Benchmarking Pv3Rs

In this document, we investigate the runtime scaling of the Pv3Rs’ main function, compute_posterior, with respect to the number of markers, the MOIs, and the number of episodes. Each timing result is replicated 30 times to account for variability.

Setup

library(Pv3Rs)
library(tictoc)
library(gtools)

# simulate allele frequencies for one marker
sim_fs_single <- function(n_a) {
  alleles <- letters[1:n_a] # n_a <= 26
  fs_unnamed <- as.vector(rdirichlet(1, alpha = rep(1, n_a)))
  setNames(fs_unnamed, alleles)
}

# simulate allele frequencies for multiple markers
# assumes each marker has the same number of alleles
sim_fs <- function(n_m, n_a) {
  markers <- paste0("m", 1:n_m) # marker names
  n_a_vec <- setNames(rep(n_a, n_m), markers)
  lapply(n_a_vec, sim_fs_single)
}

# simulate data for one marker, one episode
# sample without replacement to match desired MOI, so must have length(fs) >= MOI
sim_data_single <- function(fs_single, MOI) {
  sample(names(fs_single), MOI, prob=fs_single)
}

# simulate data for all markers, all episodes
sim_data <- function(MOIs, n_m, n_a) {
  fs <- sim_fs(n_m, n_a)
  y <- lapply(
    MOIs,
    function(MOI) lapply(fs, sim_data_single, MOI) # sample data for one episode
  )
  return(list(y=y, fs=fs))
}

Runtime vs number of markers

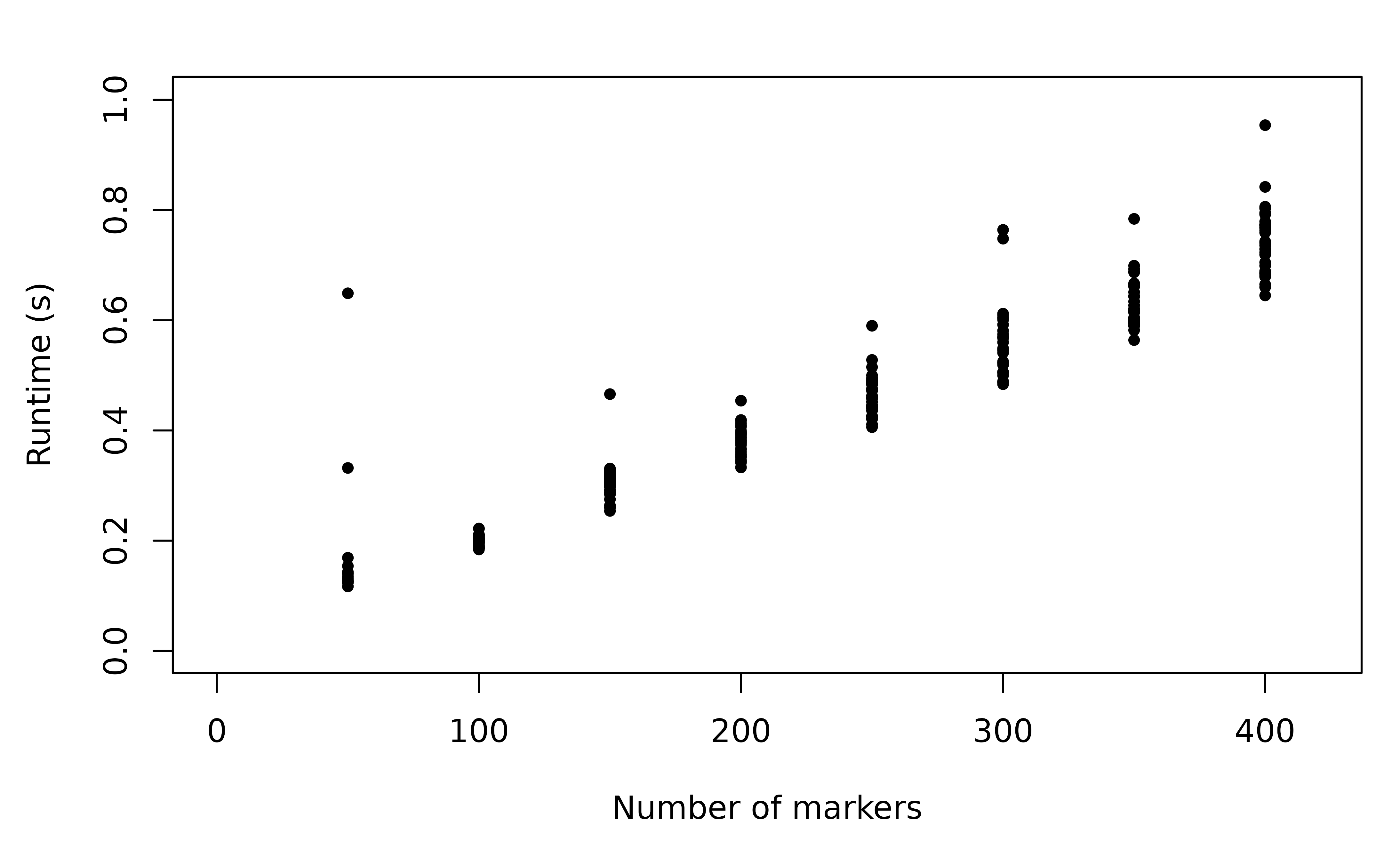
We expect the runtime of compute_posterior to scale linearly with the number of markers due to the likelihood decomposition (Section 3.4 of Taylor, Foo & White, 2022). We simulate genetic data spanning across 2 episodes both with MOI 2, and vary the number of markers between $50, 100, \ldots, 400$. Each marker is assumed to have 8 possible alleles.

set.seed(1)
n_markers <- 50*(1:8)
n_a <- 8
MOIs <- c(2, 2)
n_rep <- 30

data_by_m <- list()
for (n_m in n_markers) {
  data_by_m[[as.character(n_m)]] <- lapply(
    1:n_rep,
    function(x) sim_data(MOIs, n_m, n_a)
  )
}

time_by_m <- list()
for (n_m in n_markers) {
  time_by_m[[as.character(n_m)]] <- sapply(
    data_by_m[[as.character(n_m)]],
    function(data) {
      tic("")
      suppressMessages(compute_posterior(data$y, data$fs))
      res <- toc(quiet=TRUE)
      res$toc - res$tic
    }
  )
}

max_time <- max(sapply(time_by_m, max))
par(cex=1.0, mar=c(5, 4.5, 2, 1))
plot(
  NULL, type="n", 
  xlim=c(0, 420), 
  ylim=c(0, max_time*1.05),
  xlab="Number of markers",
  ylab="Runtime (s)"
)
for(n_m in n_markers) {
  points(rep(n_m, n_rep), time_by_m[[as.character(n_m)]], pch=20)
}

Runtime vs MOIs

As the number of MOIs increase, the runtime increases due to having more possibilities for allele assignment and more valid relationship graphs. We simulate genetic data consisting of 1 marker (8 alleles), spanning 2 episodes of various MOI combinations.

set.seed(1)
n_m <- 1
n_a <- 8
MOIs_comb <- list()
for(MOItot in 3:7) {
  for(MOI1 in (MOItot-1):1) {
    MOI2 <- MOItot-MOI1
    if(MOI1 >= MOI2) MOIs_comb <- c(MOIs_comb, list(c(MOI1, MOI2)))
  }
}
n_rep <- 30

data_by_MOI <- list()
for (MOIs in MOIs_comb) {
  data_by_MOI[[paste(MOIs, collapse=",")]] <- lapply(
    1:n_rep,
    function(x) sim_data(MOIs, n_m, n_a)
  )
}

time_by_MOI <- list()
for (MOIs in MOIs_comb) {
  MOIstr <- paste(MOIs, collapse=",")
  time_by_MOI[[MOIstr]] <- sapply(
    data_by_MOI[[MOIstr]],
    function(data) {
      tic("")
      suppressMessages(compute_posterior(data$y, data$fs))
      res <- toc(quiet=TRUE)
      res$toc - res$tic
    }
  )
}

min_time <- min(sapply(time_by_MOI, min))
max_time <- max(sapply(time_by_MOI, max))
n <- length(MOIs_comb)

par(cex=1.0, cex.axis=0.8, mar=c(5, 4.5, 2, 1))
plot(
  1, 1, type="n", 
  xlim=c(0.5, n+0.5), 
  ylim=c(min_time*0.5, max_time*2),
  xlab="MOIs",
  ylab="Runtime (s)",
  xaxt='n', log="y",
)
axis(
  side=1, at=1:n,
  sapply(MOIs_comb, paste, collapse=",")
)

for(i in 1:n) {
  points(rep(i, n_rep), time_by_MOI[[i]], pch=20)
}

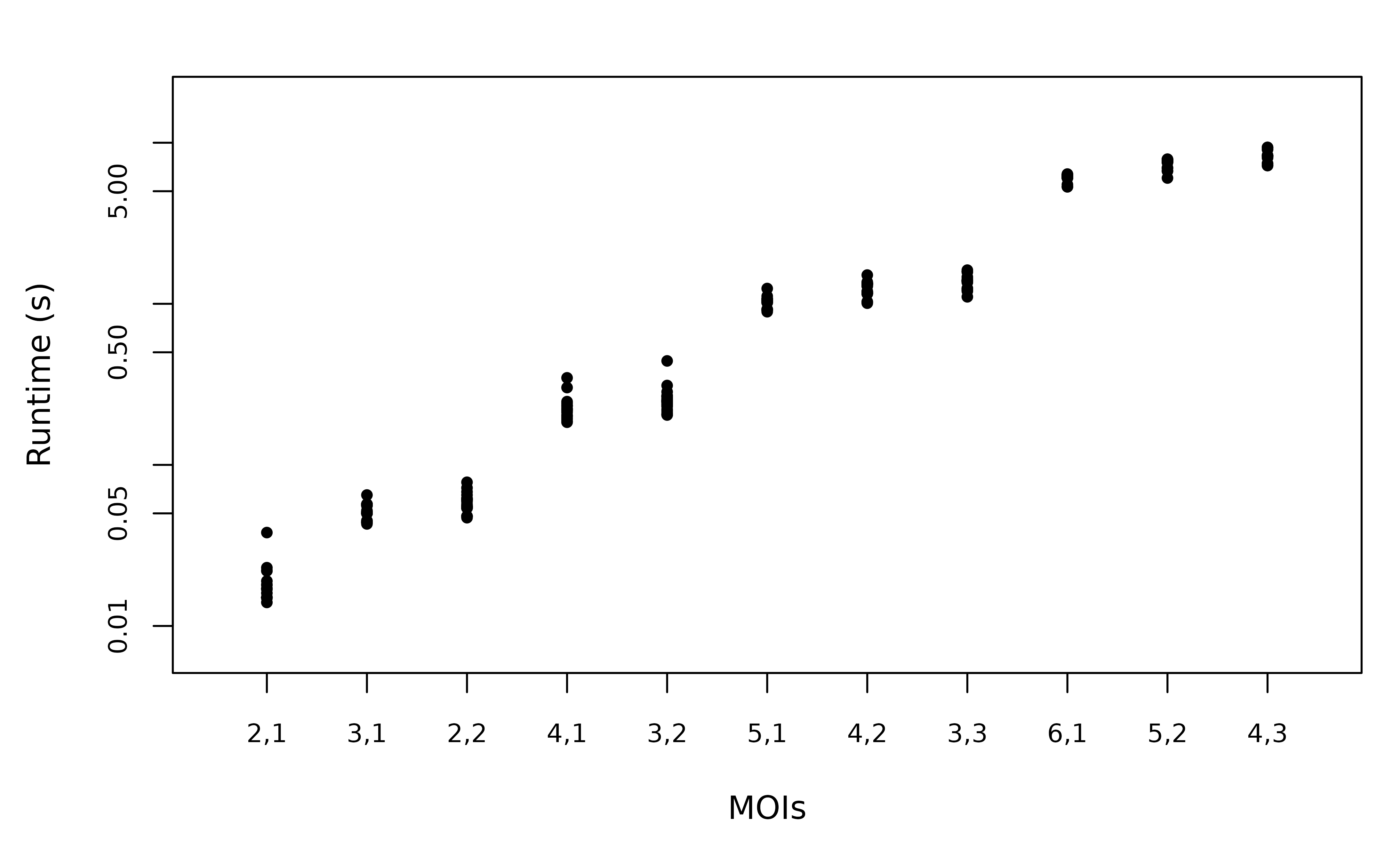
Empirically, the runtime (note the log scale) has roughly exponentially scaling with respect to the total MOI. It is difficult to conclude an exact growth rate due to the small range of the total MOI. Given a fixed total MOI, the runtime is slightly shorter (see printed output of total runtime) if the maximum MOI is larger. This can be explained by the following observations:

• A larger maximum MOI leads to more pairs of genotypes that cannot be clones. This leads to fewer valid relationship graphs to enumerate.

• Allele assignment for the largest MOI is always fixed. A smaller minimum MOI leads to fewer allele assignment possibilities to be considered.

Runtime vs number of episodes

Here we investigate two separate cases:

• increasing the number of episodes with 1 genotype per episode, and

• increasing the number of episodes with a fixed total MOI.

One genotype per episode (episodes with MOI = 1)

We simulate genetic data consisting of one marker (eight alleles), with one genotype per episode for various numbers of episodes.

set.seed(1)
n_m <- 1
n_a <- 8
n_epis <- 2:7
n_rep <- 30

data_by_epi <- list()
for (epi in n_epis) {
  data_by_epi[[as.character(epi)]] <- lapply(
    1:n_rep,
    function(x) sim_data(rep(1, epi), n_m, n_a)
  )
}

time_by_epi <- list()
for (epi in n_epis) {
  time_by_epi[[as.character(epi)]] <- sapply(
    data_by_epi[[as.character(epi)]],
    function(data) {
      tic("")
      suppressMessages(compute_posterior(data$y, data$fs))
      res <- toc(quiet=TRUE)
      res$toc - res$tic
    }
  )
}

min_time <- min(sapply(time_by_epi, min))
max_time <- max(sapply(time_by_epi, max))

par(cex=1.0, mar=c(5, 4.5, 2, 1))
plot(
  1, 1, type="n", 
  xlim=c(1.5, 7.5), 
  ylim=c(min_time*0.5, max_time*2),
  xlab="Number of monoclonal episodes",
  ylab="Runtime (s)",
  log="y",
)

for(epi in n_epis) {
  points(rep(epi, n_rep), time_by_epi[[as.character(epi)]], pch=20)
}

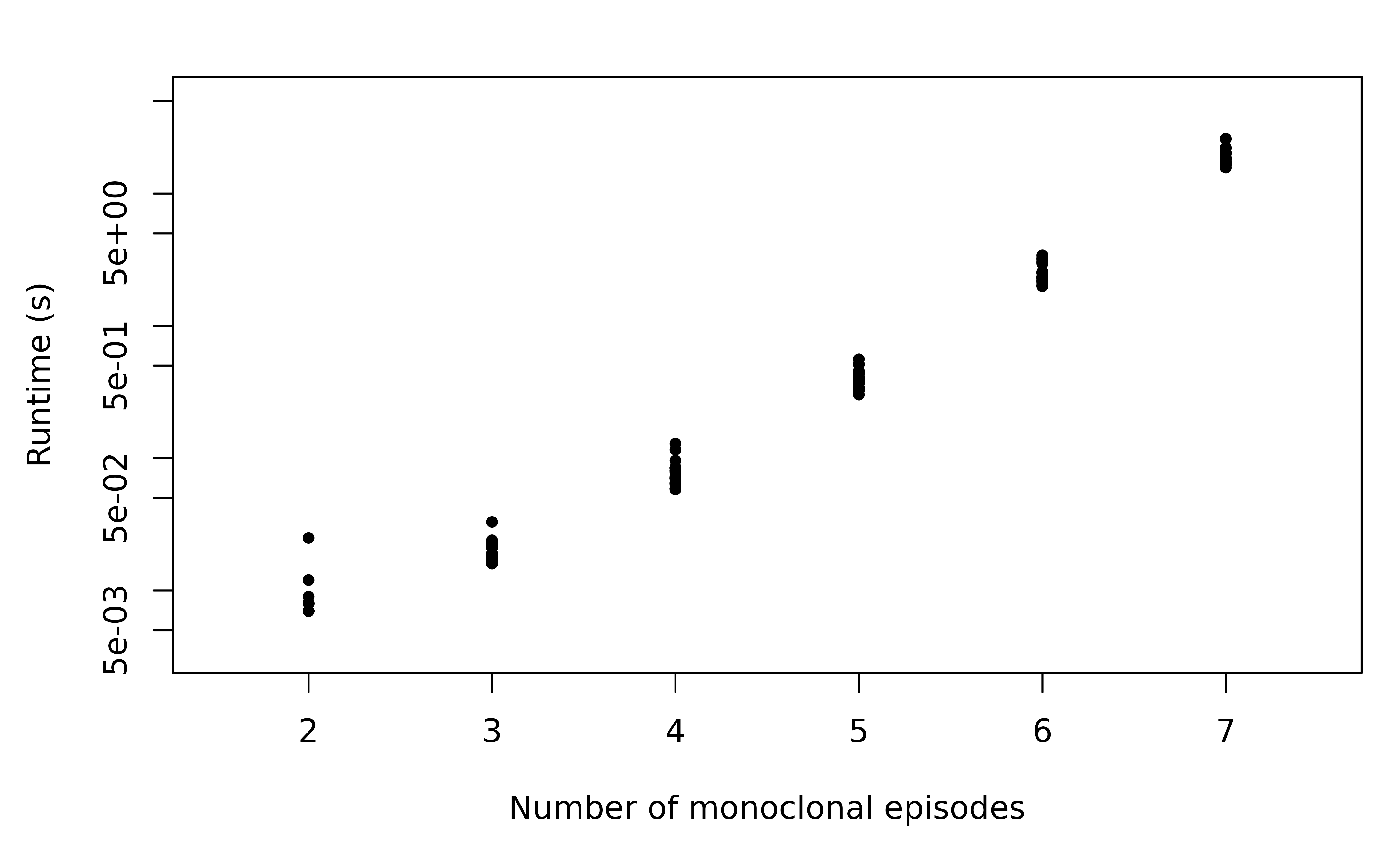
With one genotype per episode, the runtime (note the log scale) scales super-exponentially with respect to the number of episodes (or equivalently, the total MOI). In fact, the number of relationship graphs with $n$ episodes with one genotype per episode is given by $$R_n = \sum_{k=1}^n S(n,k)B_k,$$ where $S(n_k)$ are Stirling numbers of the second kind and $B_k$ are Bell numbers. We provide the derivation in the Appendix, where we also show that $\log R_n \sim n\log n$.

Fixed total MOI

We simulate genetic data consisting of one marker (8 alleles), for various numbers of episodes with a fixed total MOI of seven. See printed output below for the sequence of MOIs considered.

set.seed(1)
n_m <- 1
n_a <- 8
maxepi <- 7 # fixed total MOI
n_rep <- 30

MOI_fix_comb <- list()
for(epi in 2:maxepi) {
  m <- maxepi %/% epi
  rem <- maxepi %% epi
  MOI_fix_comb <- c(MOI_fix_comb, list(c(rep(m+1, rem), rep(m, epi-rem))))
}

data_by_MOI_fix <- list()
for (MOIs in MOI_fix_comb) {
  data_by_MOI_fix[[paste(MOIs, collapse=",")]] <- lapply(
    1:n_rep,
    function(x) sim_data(MOIs, n_m, n_a)
  )
}

time_by_MOI_fix <- list()
for (MOIs in MOI_fix_comb) {
  MOIstr <- paste(MOIs, collapse=",")
  time_by_MOI_fix[[MOIstr]] <- sapply(
    data_by_MOI_fix[[MOIstr]],
    function(data) {
      tic("")
      suppressMessages(compute_posterior(data$y, data$fs))
      res <- toc(quiet=TRUE)
      res$toc - res$tic
    }
  )
}

min_time <- min(sapply(time_by_MOI_fix, min))
max_time <- max(sapply(time_by_MOI_fix, max))

par(cex=1.0, mar=c(5, 4.5, 2, 1))
plot(
  1, 1, type="n", 
  xlim=c(1.5, maxepi + 0.5), 
  ylim=c(0, max_time*1.05),
  xlab="Number of episodes (fixed total MOI)",
  ylab="Runtime (s)",
)

for(epi in 2:maxepi) {
  points(rep(epi, n_rep), time_by_MOI_fix[[epi-1]], pch=20)
}

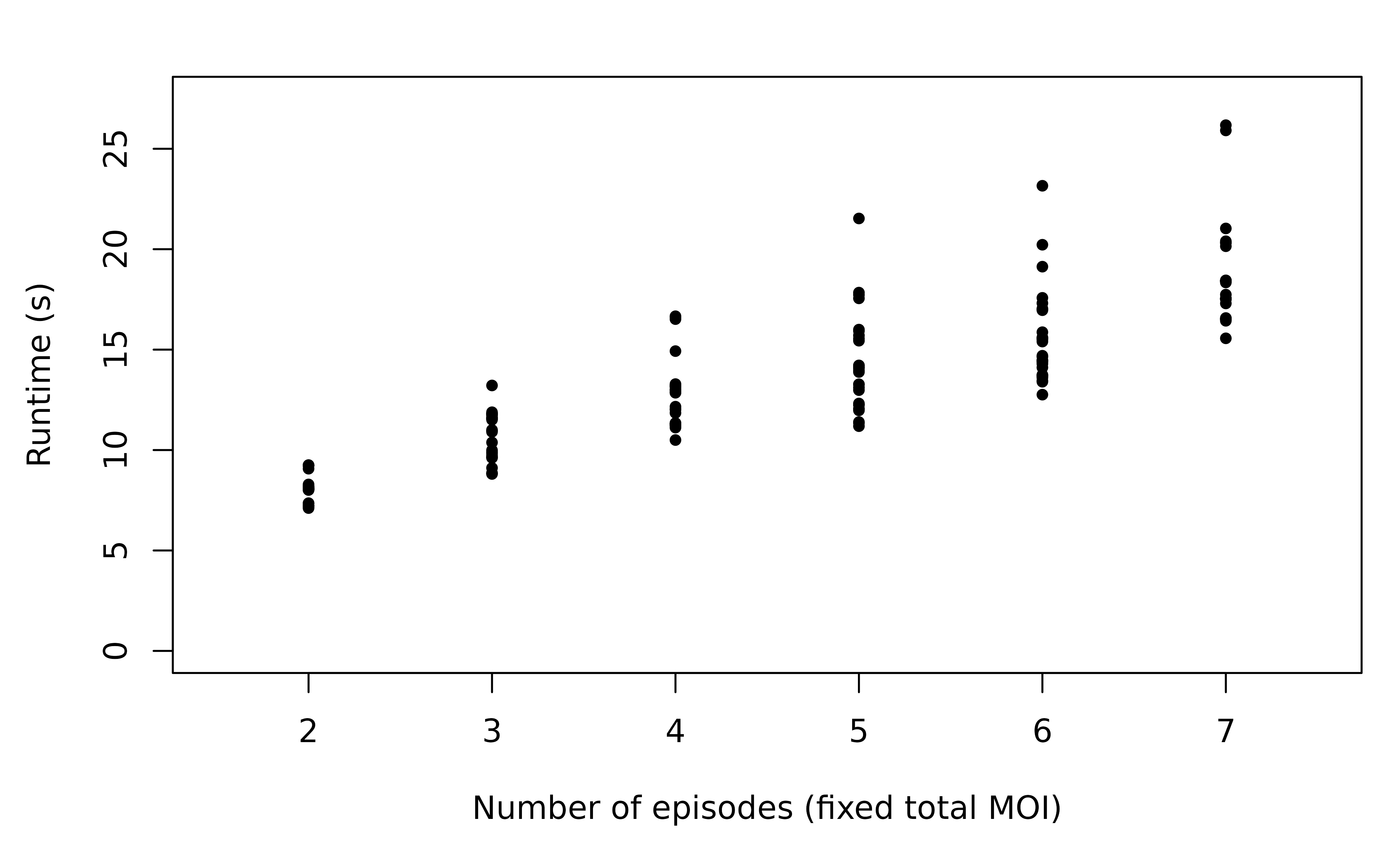
With the total MOI fixed, the runtime does not increase as drastically with the number of episodes (note linear scale, not log scale). However, more episodes still lead to more valid relationship graphs as there are more pairs that can be clones, explaining the increase in runtime.

Appendix

To derive a formula for $R_n$, the number of relationship graphs for $n$ episodes with one genotype per episode, we treat a relationship graph as a nested partition. The clonal relationships in a relationship graph induce a partition of all genotypes into subsets, where all genotypes within the same subset are clones of each other. We call such a subset a `clonal cell’. The sibling relationships in a relationship graph induce a partition of all clonal cells into subsets, such that any two genotypes from the same subset that are not clones of each other must be siblings. Recall that Stirling numbers of the second kind $S(n,k)$ count the number of ways to partition $n$ objects into $k$ subsets, whereas the Bell numbers $B_k$ count the number of ways to partition $k$ objects (into any number of subsets). Letting $k$ denote the number of clonal cells, we have $$R_n = \sum_{k=1}^n S(n,k)B_k.$$

To establish the asymptotics of $R_n$, we first note that $R_n \ge S(n,n)B_n = B_n$. It is well known that $\log B_n \sim n\log n$. If we additionally have that $R_n \le n^n$, it then follows that $\log R_n \sim n\log n$. The rest of this appendix is devoted to proving that $R_n \le n^n$ is indeed true. Let $\mathcal{H}_n$ be the set of all functions $h$ that map elements of $\{1,\ldots,n\}$ to $\{1,\ldots,n\}$. Since $|\mathcal{H}_n|=n^n$, it suffices to show that there is an injection from the set of all relationship graphs (with $n$ genotypes) to $\mathcal{H}_n$.

Consider the following mapping of a relationship graph to a function $h$: Given a relationship graph, label the genotypes from $1$ to $n$, and label the clonal cells from $1$ to $k$. For each $k'=1,\ldots,k$, let $c_{k'}$ denote the smallest genotype label in clonal cell $k'$. For each genotype $i$ in clonal cell $k'$ that is not $c_{k'}$, we define $h(i)=c_{k'}$. It remains to define the values of $h(c_1),\ldots,h(c_k)$. The sibling relationships induce a partition of $\{1,\ldots,k\}$ into subsets of clonal cells. Let $\{x_1,\ldots,x_m\}$ be such a subset, where $1\le x_1 \le \cdots \le x_m\le k$. For each $m'=1,\ldots,m$, we define $h(c_{x_{m'}})=c_{x_{m'+1}}$, where subscripts of $x$ are taken modulo $m$. We repeat the same for all subsets of the partition induced by sibling relationships, which completes the definition of the mapping. Informally, we select one genotype from each clonal cell to be a representative. The function $h$ maps non-representative genotypes to their corresponding representatives, and maps representative genotypes to representative genotypes, such that each subset induced by the sibling relationships corresponds to a cycle induced by $h$.

It remains to show that this mapping is indeed an injection. Consider two different relationship graphs $g_1$ and $g_2$, corresponding to the functions $h_1$ and $h_2$ under the mapping above. We seek to show that $h_1\neq h_2$. Suppose that the genotypes $i$ and $i'$ have a different relationship under $g_1$ and $g_2$. It suffices to consider the following two cases:

Case 1: Genotypes $i$ and $i'$ are strangers under one of $g_1$ and $g_2$, but not under the other graph. Given a function $h$ obtained from the mapping of a relationship graph and a genotype $j$, let $\textrm{sink}(j;h)$ denote the set of genotype labels that appear infinitely many times in the sequence $(j,h(j),h(h(j)),\ldots)$. It follows that $\textrm{sink}(i;h)\neq \textrm{sink}(i';h)$ if and only if genotypes $i$ and $i'$ are strangers. Therefore, we must have $h_1\neq h_2$.

Case 2: Genotypes $i$ and $i'$ are siblings under one of $g_1$ and $g_2$, but are clones under the other graph. Given a function $h$ obtained from the mapping of a relationship graph and a genotype $j$, let $\textrm{sink}_1(j;h)$ be the genotype label in $\textrm{sink}(j;h)$ that occurs first in the sequence $(j,h(j),h(h(j)),\ldots)$. It follows that $\textrm{sink}_1(i;h)= \textrm{sink}_1(i';h)$ if and only if genotypes $i$ and $i'$ are clones (or if $i=i'$, which is irrelevant). Therefore, we must have $h_1\neq h_2$.

This completes the proof that $\log R_n \sim n\log n$.